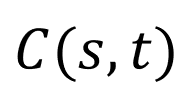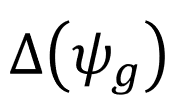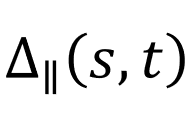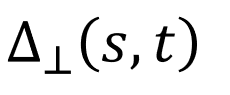Nutation Simulator

This simulator has been realised to give a visual understanding in 3 dimensions of plants nutation, the circular movements of plants during their development. The driver of the movement, the differential growth is related to the curvature of the plants through the following equation

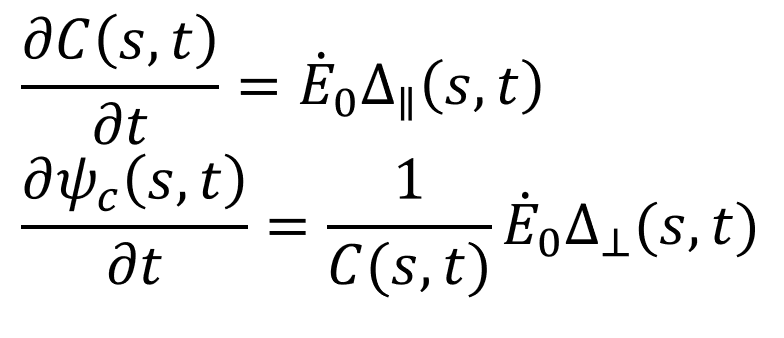
An internal oscillator is driving the movement by constantly switching the directon of the growth differential

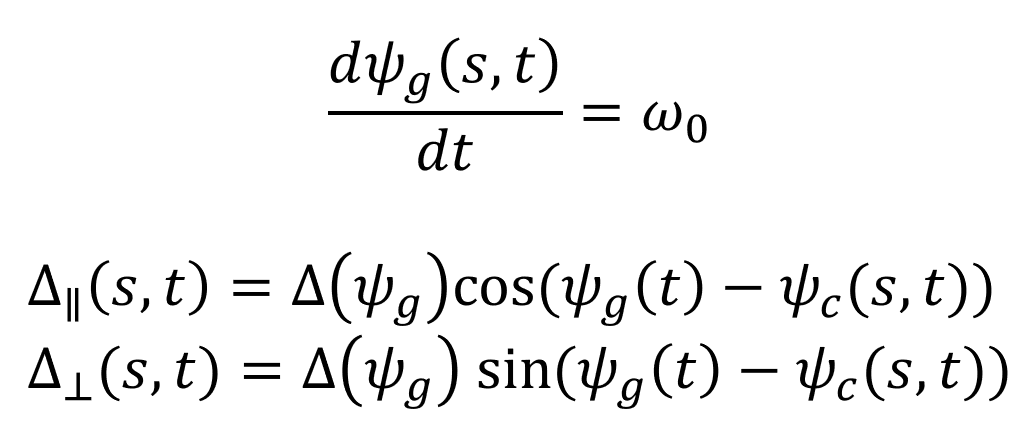
Finally elongation can be introduced by an increase of the length of each element of the stem over time

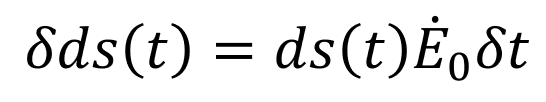
And the elongation can be limited to a subapical zone

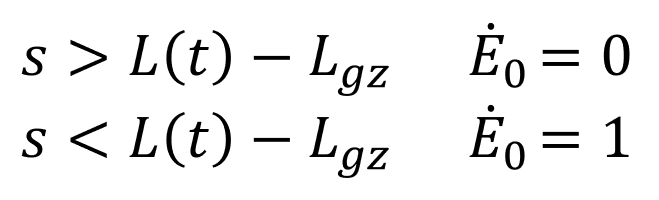
Pre Defined Solutions

A set of pre-defined solutions can be accessed with the key numbers (0-5). They provide an instantaneous access to the pattern observed with the simulator

Key
0

Circular pattern centered around the base of the organ
1

Circular pattern not centered around the base of the organ
2

No rotation of the principal direction of the growth differentual
3

Influence of proprioception on a circular pattern not centered around the base of the organ
4

Influence of proprioception and elongation on a circular pattern not centered around the base of the organ
5

Influence of proprioception and subapical elongationon a circular pattern not centered around the base of the organ

Parameters

Curvilinear abscissa along the organ

Time

Length of the organ

Length of the growth zone

Curvature

Relative Elemental Growth Rate (REGR)

Principal direction of curvature

Principal direction of the growth differential

Angular velocity of the growth differential

Frequency of the angular velocity

Proprioception

REGR in the principal direction of the growth differential

REGR in the principal direction of curvature

REGR in the direction orthotgonal to the principal direction of curvature

Reference

Bastien, R. and Meroz, Y., 2016. The Dynamics of Plant Nutation Result From the Slaving of Curvature to the Orientation of Differential Growth. arXiv preprint arXiv:1603.00459.

Source Code